同學可以利用此項 小技能
來做像是移動某個物體到一個影像畫面的特定一個區塊
然後顯示一些文字或是警示圖片等 小互動

最後效果
RGB色彩空間調整二值化門檻值
----> 缺點 : 受 光源影響
座標數值的獲得
觀察
HSV色彩空間效果
雜訊的除去技巧
開運算
先侵蝕
後膨脹
可以看到 不像RGB空間
把顏色轉為HSV空間效果 較好
用到的 API function
霍夫圓偵測

霍夫圓偵測的原理
霍夫轉換 (Hough Transform )
----> 只應用在影像處理中的轉換!!!!!
未來可能各位有機會學到的
傅立葉轉換
離散餘弦轉換
小波轉換
主成分分析
----> 在各行各業 都有機會用到 不單單在影像領域
土木工程、機械工程、通訊、電機 都常碰到
統計學上、資料分析上 ===> PCA
最早被提出來主要是應用在直線偵測(Line Detection)用的
於1962年由P.Hough
(P.V.C. Hough. Method and Means for Recognizing Complex Patterns, US Patent 3,069,654, December 1962)提出,
繼而於1972年首度以論文形式發表
(R.O.Duda, R.E.Hart. Use of the Hough Transform to Detect Lines and Curves in Pictures, CACM(15). No. 1, January 1972, pp. 11-15.)
用在二值化影像的特定形狀偵測(shape detection)
主要原理是利用影像中分散的點位置找出特定形狀(例如直線或圓)的參數值,
每一個點藉由一對多的映射(由影像(位置)空間映射到參數空間)
產生參數的所有可能值,再累計全部點所產生的參數值,
最後在得以在參數空間決定表現最明顯的形狀參數。
你會問 捨麼是 位置空間
以前國高中有學過一個數學式
叫做 y = ax + b
你再回過頭 想想看
一張畫著一條線的影像
一張影像中 有一條線
只要我們能夠找到 此條線的 a 跟 b
就能分別 得到 其 方向 跟 位置
霍夫轉換目的就是 先定義好 一個數學公式
來求得 a 跟 b 兩個數值
一張有一條線的影像 通常 我們人一看就可以有這感覺
它就是一條直線 是一條可以寫成 y = ax+b 直線方程式的線段
是一條由很多連續的點 串起來的一條線的關係
因為你的肉眼是同時看到所有在這條線上的所有點的!!!!
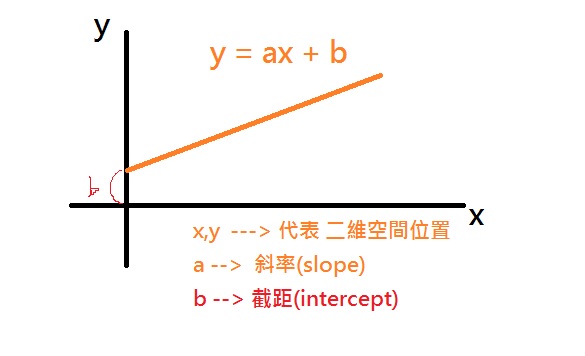
直線方程式 : y = ax+b
x , y ---> 變數 代表 空間位置
a : 斜率 跟 b :截距 ---> 參數
一張畫著一個圓的影像
圓方程式: (X-Xc)^2 + (Y-Yc)^2 = R^2
圓心 : (Xc,Yc)
半徑 ; R
X 、 Y ---> 變數 用來描述空間位置
圓心 : (Xc,Yc) 跟 半徑 ; R ---> 參數
目標去找到 這些參數
但是 電腦的眼睛不像人眼般聰明
電腦是一個像素 一個 像素的看
電腦是看不到這些像素之共同關係的!!!!!
因此 霍夫轉換 就是為此而產生
電腦先是以掃描方式 紀錄每個 pixel 的微量資訊 在 慢慢一個一個保留
微量資訊 最後就拿來經由判出
一般人肉眼一看就知道的 直線 或 圓 喔 !!!!
霍夫轉換示意圖
以直線偵測來說

位置空間 =====> 參數空間
X,Y 本來是一個點座標 ----- 經霍夫轉換-----------> (X變斜率,Y變截距)
一個公式(在保持不變的前提下)進行轉換獲得參數
腦筋會轉不過來有點難懂的部分
Point1.
位置空間中的一個點 映射 到 參數空間中 就會變成一條線
參數空間中的一個點 也會在映射到位置空間中 變成一條線
Point2.
在位置空間中的一條線上N個點 映射到 參數空間 會變成一條線
在參數空間中 N 條 線 必定交於同一個點
以圓形偵測來說
Case1. 已知半徑為 k(常數)
位置空間
(X - C1)^2 + (Y - C2)^2 = k^2
從影像當中找 已知半徑為k的 圓位置
在程式中應用到的是我設置一個範圍在
最小半徑: 10
最大半徑: 400
在一個不停更新的畫面中可能會出現不一樣大小的圓形範圍
可能是受到光源影響
也可能是又多出一個圓型物件在畫面上
Case2. 對於未知半徑的圓
位置空間
一個點 ----轉成----> 一個圓錐曲面
(雙圓錐面 是指 可以准許C3為負值)
每一個點轉過去參數空間 相當於一個 圓錐(曲)面
假設左邊位置空間的圓 是由 100個 點組成 我們就可以 轉出 100個 圓錐曲面
藉此取得 100個圓錐曲面的 交點 -----> 相當於 圓的圓心及半徑
參數愈多 ---> 霍夫轉換效率愈差喔!!!!
那有些艱深的數學可以請教老師喔 恩恩 !!
這部分針對原理做一個簡單介紹













沒有留言:
張貼留言